Physics:Physics-informed neural networks

From HandWiki
Short description: Technique to solve partial differential equations
Physics-informed neural networks for solving Navier–Stokes equations

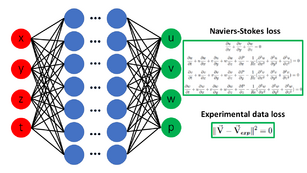
Physics-informed neural networks (PINNs) are a type of universal function approximators that can embed the knowledge of any physical laws that govern a given data-set in the learning process, and can be described by partial differential equations (PDEs).[1] They overcome the low data availability of some biological and engineering systems that makes most state-of-the-art machine learning techniques lack robustness, rendering them ineffective in these scenarios.[1] The prior knowledge of general physical laws acts in the training of neural networks (NNs) as a regularization agent that limits the space of admissible solutions, increasing the correctness of the function approximation. This way, embedding this prior information into a neural network results in enhancing the information content of the available data, facilitating the learning algorithm to capture the right solution and to generalize well even with a low amount of training examples.

Function approximation

Most of the physical laws that govern the dynamics of a system can be described by partial differential equations. For example, the Navier–Stokes equations[2] are a set of partial differential equations derived from the conservation laws (i.e., conservation of mass, momentum, and energy) that govern fluid mechanics. The solution of the Navier–Stokes equations with appropriate initial and boundary conditions allows the quantification of flow dynamics in a precisely defined geometry. However, these equations cannot be solved exactly and therefore numerical methods must be used (such as finite differences, finite elements and finite volumes). In this setting, these governing equations must be solved while accounting for prior assumptions, linearization, and adequate time and space discretization.

Recently, solving the governing partial differential equations of physical phenomena using deep learning has emerged as a new field of scientific machine learning (SciML), leveraging the universal approximation theorem[3] and high expressivity of neural networks. In general, deep neural networks could approximate any high-dimensional function given that sufficient training data are supplied.[4] However, such networks do not consider the physical characteristics underlying the problem, and the level of approximation accuracy provided by them is still heavily dependent on careful specifications of the problem geometry as well as the initial and boundary conditions. Without this preliminary information, the solution is not unique and may lose physical correctness. On the other hand, physics-informed neural networks (PINNs) leverage governing physical equations in neural network training. Namely, PINNs are designed to be trained to satisfy the given training data as well as the imposed governing equations. In this fashion, a neural network can be guided with training data that do not necessarily need to be large and complete.[4] Potentially, an accurate solution of partial differential equations can be found without knowing the boundary conditions.[5] Therefore, with some knowledge about the physical characteristics of the problem and some form of training data (even sparse and incomplete), PINN may be used for finding an optimal solution with high fidelity.

PINNs allow for addressing a wide range of problems in computational science and represent a pioneering technology leading to the development of new classes of numerical solvers for PDEs. PINNs can be thought of as a meshfree alternative to traditional approaches (e.g., CFD for fluid dynamics), and new data-driven approaches for model inversion and system identification.[6] Notably, the trained PINN network can be used for predicting the values on simulation grids of different resolutions without the need to be retrained.[7] In addition, they allow for exploiting automatic differentiation (AD)[8] to compute the required derivatives in the partial differential equations, a new class of differentiation techniques widely used to derive neural networks assessed to be superior to numerical or symbolic differentiation.

Modeling and computation

A general nonlinear partial differential equation can be:

[math]\displaystyle{ u_t + N[u; \lambda]=0, \quad x \in \Omega, \quad t \in[0, T] }[/math]

where [math]\displaystyle{ u(t,x) }[/math] denotes the solution, [math]\displaystyle{ N[\cdot; \lambda] }[/math] is a nonlinear operator parametrized by [math]\displaystyle{ \lambda }[/math], and [math]\displaystyle{ \Omega }[/math] is a subset of [math]\displaystyle{ \mathbb{R}^{D} }[/math]. This general form of governing equations summarizes a wide range of problems in mathematical physics, such as conservative laws, diffusion process, advection-diffusion systems, and kinetic equations. Given noisy measurements of a generic dynamic system described by the equation above, PINNs can be designed to solve two classes of problems:

  • data-driven solution
  • data-driven discovery

of partial differential equations.

Data-driven solution of partial differential equations

The data-driven solution of PDE[1] computes the hidden state [math]\displaystyle{ u(t,x) }[/math] of the system given boundary data and/or measurements [math]\displaystyle{ z }[/math], and fixed model parameters [math]\displaystyle{ \lambda }[/math]. We solve:

[math]\displaystyle{ u_t + N[u]=0, \quad x \in \Omega, \quad t \in[0, T] }[/math].

By defining the residual [math]\displaystyle{ f(t,x) }[/math] as

[math]\displaystyle{ f := u_t + N[u]=0 }[/math],

and approximating [math]\displaystyle{ u(t,x) }[/math] by a deep neural network. This network can be differentiated using automatic differentiation. The parameters of [math]\displaystyle{ u(t,x) }[/math] and [math]\displaystyle{ f(t,x) }[/math] can be then learned by minimizing the following loss function [math]\displaystyle{ L_{tot} }[/math]:

[math]\displaystyle{ L_{tot} = L_{u} + L_{f} }[/math].

Where [math]\displaystyle{ L_{u} = \Vert u-z\Vert_{\Gamma} }[/math] is the error between the PINN [math]\displaystyle{ u(t, x) }[/math] and the set of boundary conditions and measured data on the set of points [math]\displaystyle{ \Gamma }[/math] where the boundary conditions and data are defined, and [math]\displaystyle{ L_{f} = \Vert f\Vert_{\Gamma} }[/math] is the mean-squared error of the residual function. This second term encourages the PINN to learn the structural information expressed by the partial differential equation during the training process.

This approach has been used to yield computationally efficient physics-informed surrogate models with applications in the forecasting of physical processes, modeling predictive control, multi-physics and multi-scale modeling, and simulation.[9] It has been shown to converge to the solution of the PDE.[10]

Data-driven discovery of partial differential equations

Given noisy and incomplete measurements [math]\displaystyle{ z }[/math] of the state of the system, the data-driven discovery of PDE[6] results in computing the unknown state [math]\displaystyle{ u(t,x) }[/math] and learning model parameters [math]\displaystyle{ \lambda }[/math] that best describe the observed data and it reads as follows:

[math]\displaystyle{ u_t + N[u; \lambda]=0, \quad x \in \Omega, \quad t \in[0, T] }[/math].

By defining [math]\displaystyle{ f(t,x) }[/math] as

[math]\displaystyle{ f := u_t + N[u; \lambda]=0 }[/math],

and approximating [math]\displaystyle{ u(t,x) }[/math] by a deep neural network, [math]\displaystyle{ f(t,x) }[/math] results in a PINN. This network can be derived using automatic differentiation. The parameters of [math]\displaystyle{ u(t,x) }[/math] and [math]\displaystyle{ f(t,x) }[/math], together with the parameter [math]\displaystyle{ \lambda }[/math] of the differential operator can be then learned by minimizing the following loss function [math]\displaystyle{ L_{tot} }[/math]:

[math]\displaystyle{ L_{tot} = L_{u} + L_{f} }[/math].

Where [math]\displaystyle{ L_{u} = \Vert u-z\Vert_{\Gamma} }[/math], with [math]\displaystyle{ u }[/math] and [math]\displaystyle{ z }[/math] state solutions and measurements at sparse location [math]\displaystyle{ \Gamma }[/math], respectively and [math]\displaystyle{ L_{f} = \Vert f\Vert_{\Gamma} }[/math] residual function. This second term requires the structured information represented by the partial differential equations to be satisfied in the training process.

This strategy allows for discovering dynamic models described by nonlinear PDEs assembling computationally efficient and fully differentiable surrogate models that may find application in predictive forecasting, control, and data assimilation.[11][12][13][14]

Physics-informed neural networks for piece-wise function approximation

PINN is unable to approximate PDEs that have strong non-linearity or sharp gradients that commonly occur in practical fluid flow problems. Piece-wise approximation has been an old practice in the field of numerical approximation. With the capability of approximating strong non-linearity extremely light weight PINNs are used to solve PDEs in much larger discrete subdomains that increases accuracy substantially and decreases computational load as well.[15][16] DPINN (Distributed physics-informed neural networks) and DPIELM (Distributed physics-informed extreme learning machines) are generalizable space-time domain discretization for better approximation.[15] DPIELM is an extremely fast and lightweight approximator with competitive accuracy. Domain scaling on the top has a special effect.[16] Another school of thought is discretization for parallel computation to leverage usage of available computational resources.

XPINNs[17] is a generalized space-time domain decomposition approach for the physics-informed neural networks (PINNs) to solve nonlinear partial differential equations on arbitrary complex-geometry domains. The XPINNs further pushes the boundaries of both PINNs as well as Conservative PINNs (cPINNs),[18] which is a spatial domain decomposition approach in the PINN framework tailored to conservation laws. Compared to PINN, the XPINN method has large representation and parallelization capacity due to the inherent property of deployment of multiple neural networks in the smaller subdomains. Unlike cPINN, XPINN can be extended to any type of PDEs. Moreover, the domain can be decomposed in any arbitrary way (in space and time), which is not possible in cPINN. Thus, XPINN offers both space and time parallelization, thereby reducing the training cost more effectively. The XPINN is particularly effective for the large-scale problems (involving large data set) as well as for the high-dimensional problems where single network based PINN is not adequate. The rigorous bounds on the errors resulting from the approximation of the nonlinear PDEs (incompressible Navier–Stokes equations) with PINNs and XPINNs are proved.[14]

Physics-informed neural networks and functional interpolation

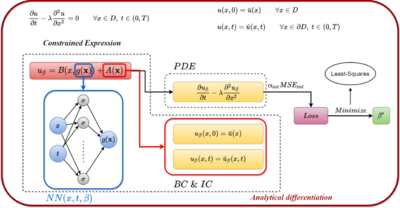
X-TFC framework scheme for PDE solution learning

In the PINN framework, initial and boundary conditions are not analytically satisfied, thus they need to be included in the loss function of the network to be simultaneously learned with the differential equation (DE) unknown functions. Having competing objectives during the network's training can lead to unbalanced gradients while using gradient-based techniques, which causes PINNs to often struggle to accurately learn the underlying DE solution. This drawback is overcome by using functional interpolation techniques such as the Theory of Functional Connections (TFC)'s constrained expression, in the Deep-TFC framework, which reduces the solution search space of constrained problems to the subspace of neural network that analytically satisfies the constraints.[19] A further improvement of PINN and functional interpolation approach is given by the Extreme Theory of Functional Connections (X-TFC) framework, where a single-layer Neural Network and the extreme learning machine training algorithm are employed.[20] X-TFC allows to improve the accuracy and performance of regular PINNs, and its robustness and reliability are proved for stiff problems, optimal control, aerospace, and rarefied gas dynamics applications.[21][22][23]

Physics-informed PointNet (PIPN) for multiple sets of irregular geometries

Regular PINNs are only able to obtain the solution of a forward or inverse problem on a single geometry. It means that for any new geometry (computational domain), one must retrain a PINN. This limitation of regular PINNs imposes high computational costs, specifically for a comprehensive investigation of geometric parameters in industrial designs. Physics-informed PointNet (PIPN) [24] is fundamentally the result of a combination of PINN's loss function with PointNet.[25] In fact, instead of using a simple fully connected neural network, PIPN uses PointNet as the core of its neural network. PointNet has been primarily designed for deep learning of 3D object classification and segmentation by the research group of Leonidas J. Guibas. PointNet extracts geometric features of input computational domains in PIPN. Thus, PIPN is able to solve governing equations on multiple computational domains (rather than only a single domain) with irregular geometries, simultaneously. The effectiveness of PIPN has been shown for incompressible flow, heat transfer and linear elasticity.[24][26]

Limitations

Translation and discontinuous behavior are hard to approximate using PINNs.[15] They fail when solving differential equations with slight advective dominance.[16] The difficulty in training of PINNs in advection-dominated PDEs can be explained by Kolmogorov n–width of the solution. [27] They also fail to solve a system of dynamical systems and hence have not been a success in solving chaotic equations.[28] One of the reasons behind the failure of the regular PINNs is soft-constraining of Dirichlet and Neumann boundary conditions which pose multi-objective optimization problems. This requires the need for manually weighing the loss terms to be able to optimize. Another reason is getting optimization itself. Posing PDE solving as an optimization problem brings in all the problems that are faced in the world of optimization, the major one being getting stuck at a local optimum pretty often.[16][29]

References

  1. ↑ 1.0 1.1 1.2 Raissi, Maziar; Perdikaris, Paris; Karniadakis, George Em (2017-11-28). "Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations". arXiv:1711.10561 [cs.AI].
  2. ↑ Batchelor, G. K. (2000). An introduction to fluid dynamics (2nd pbk. ed.). Cambridge, U.K.: Cambridge University Press. ISBN 978-0-521-66396-0. 
  3. ↑ Hornik, Kurt; Tinchcombe, Maxwell; White, Halbert (1989-01-01). "Multilayer feedforward networks are universal approximators" (in en). Neural Networks 2 (5): 359–366. doi:10.1016/0893-6080(89)90020-8. ISSN 0893-6080. https://www.sciencedirect.com/science/article/abs/pii/0893608089900208. 
  4. ↑ 4.0 4.1 Arzani, Amirhossein; Dawson, Scott T. M. (2021). "Data-driven cardiovascular flow modelling: examples and opportunities". Journal of the Royal Society Interface 18 (175): 20200802. doi:10.1098/rsif.2020.0802. PMID 33561376. 
  5. ↑ Arzani, Amirhossein; Wang, Jian-Xun; D'Souza, Roshan M. (2021-06-07). "Uncovering near-wall blood flow from sparse data with physics-informed neural networks". Physics of Fluids 33 (7): 071905. doi:10.1063/5.0055600. Bibcode: 2021PhFl...33g1905A. 
  6. ↑ 6.0 6.1 Raissi, Maziar; Perdikaris, Paris; Karniadakis, George Em (2019-02-01). "Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations" (in en). Journal of Computational Physics 378: 686–707. doi:10.1016/j.jcp.2018.10.045. ISSN 0021-9991. Bibcode: 2019JCoPh.378..686R. https://www.sciencedirect.com/science/article/pii/S0021999118307125. 
  7. ↑ Markidis, Stefano (2021-03-11). "Physics-Informed Deep-Learning for Scientific Computing". arXiv:2103.09655 [math.NA].
  8. ↑ Baydin, Atilim Gunes; Pearlmutter, Barak A.; Radul, Alexey Andreyevich; Siskind, Jeffrey Mark (2018-02-05). "Automatic differentiation in machine learning: a survey". arXiv:1502.05767 [cs.SC].
  9. ↑ Raissi, Maziar; Yazdani, Alireza; Karniadakis, George Em (2018-08-13). "Hidden Fluid Mechanics: A Navier–Stokes Informed Deep Learning Framework for Assimilating Flow Visualization Data". arXiv:1808.04327 [cs.CE].
  10. ↑ Doumèche, Nathan; Biau, Gérard; Boyer, Claire (2023-05-02). "Convergence and error analysis of PINNs". arXiv:2305.01240 [math.ST].
  11. ↑ Fu, Jinlong; Xiao, Dunhui; Fu, Rui; Li, Chenfeng; Zhu, Chuanhua; Arcucci, Rossella; Navon, Ionel M. (February 2023). "Physics-data combined machine learning for parametric reduced-order modelling of nonlinear dynamical systems in small-data regimes". Computer Methods in Applied Mechanics and Engineering 404: 115771. doi:10.1016/j.cma.2022.115771. Bibcode: 2023CMAME.404k5771F. 
  12. ↑ Raissi, Maziar; Yazdani, Alireza; Karniadakis, George Em (2020-02-28). "Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations" (in en). Science 367 (6481): 1026–1030. doi:10.1126/science.aaw4741. ISSN 0036-8075. PMID 32001523. Bibcode: 2020Sci...367.1026R. 
  13. ↑ Mishra, Siddhartha; Molinaro, Roberto (2021-04-01). "Estimates on the generalization error of Physics Informed Neural Networks (PINNs) for approximating a class of inverse problems for PDEs". arXiv:2007.01138 [math.NA].
  14. ↑ 14.0 14.1 Ryck, Tim De; Jagtap, Ameya D.; Mishra, Siddhartha (2022). "Error estimates for physics informed neural networks approximating the Navier–Stokes equations". arXiv:2203.09346 [math.NA].
  15. ↑ 15.0 15.1 15.2 Dwivedi, Vikas; Parashar, Nishant; Srinivasan, Balaji (2021-01-08). "Distributed learning machines for solving forward and inverse problems in partial differential equations" (in en). Neurocomputing 420: 299–316. doi:10.1016/j.neucom.2020.09.006. ISSN 0925-2312. https://www.sciencedirect.com/science/article/pii/S0925231220314090. 
  16. ↑ 16.0 16.1 16.2 16.3 [1]Rout, Siddharth; Dwivedi, Vikas; Srinivasan, Balaji (2021). "Numerical Approximation in CFD Problems Using Physics Informed Machine Learning". arXiv:2111.02987 [cs.LG].
  17. ↑ Jagtap, Ameya D.; Karniadakis, George Em (2020). "Extended physics-informed neural networks (xpinns): A generalized space-time domain decomposition based deep learning framework for nonlinear partial differential equations". Communications in Computational Physics 28 (5): 2002–2041. doi:10.4208/cicp.OA-2020-0164. Bibcode: 2020CCoPh..28.2002K. 
  18. ↑ Jagtap, Ameya D.; Kharazmi, Ehsan; Karniadakis, George Em (2020). "Conservative Physics-Informed Neural Networks on Discrete Domains for Conservation Laws: Applications to forward and inverse problems". Computer Methods in Applied Mechanics and Engineering 365: 113028. doi:10.1016/j.cma.2020.113028. Bibcode: 2020CMAME.365k3028J. 
  19. ↑ Leake, Carl; Mortari, Daniele (12 March 2020). "Deep Theory of Functional Connections: A New Method for Estimating the Solutions of Partial Differential Equations". Machine Learning and Knowledge Extraction 2 (1): 37–55. doi:10.3390/make2010004. PMID 32478283. 
  20. ↑ Schiassi, Enrico; Furfaro, Roberto; Leake, Carl; De Florio, Mario; Johnston, Hunter; Mortari, Daniele (October 2021). "Extreme theory of functional connections: A fast physics-informed neural network method for solving ordinary and partial differential equations". Neurocomputing 457: 334–356. doi:10.1016/j.neucom.2021.06.015. 
  21. ↑ Schiassi, Enrico; De Florio, Mario; Ganapol, Barry D.; Picca, Paolo; Furfaro, Roberto (March 2022). "Physics-informed neural networks for the point kinetics equations for nuclear reactor dynamics". Annals of Nuclear Energy 167: 108833. doi:10.1016/j.anucene.2021.108833. 
  22. ↑ Schiassi, Enrico; D’Ambrosio, Andrea; Drozd, Kristofer; Curti, Fabio; Furfaro, Roberto (4 January 2022). "Physics-Informed Neural Networks for Optimal Planar Orbit Transfers". Journal of Spacecraft and Rockets 59 (3): 834–849. doi:10.2514/1.A35138. Bibcode: 2022JSpRo..59..834S. 
  23. ↑ De Florio, Mario; Schiassi, Enrico; Ganapol, Barry D.; Furfaro, Roberto (April 2021). "Physics-informed neural networks for rarefied-gas dynamics: Thermal creep flow in the Bhatnagar–Gross–Krook approximation". Physics of Fluids 33 (4): 047110. doi:10.1063/5.0046181. Bibcode: 2021PhFl...33d7110D. 
  24. ↑ 24.0 24.1 Kashefi, Ali; Mukerji, Tapan (2022). "Physics-informed PointNet: A deep learning solver for steady-state incompressible flows and thermal fields on multiple sets of irregular geometries". Journal of Computational Physics 468: 111510. doi:10.1016/j.jcp.2022.111510. Bibcode: 2022JCoPh.46811510K. 
  25. ↑ Qi, Charles; Su, Hao; Mo, Kaichun; Guibas, Leonidas (2017). "Pointnet: Deep learning on point sets for 3d classification and segmentation". Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition: 652–660. https://openaccess.thecvf.com/content_cvpr_2017/papers/Qi_PointNet_Deep_Learning_CVPR_2017_paper.pdf. 
  26. ↑ Kashefi, Ali; Mukerji, Tapan (2023). "Physics-informed PointNet: On how many irregular geometries can it solve an inverse problem simultaneously? Application to linear elasticity". arXiv:2303.13634 [cs.LG].
  27. ↑ Mojgani, Rambod; Balajewicz, Maciej; Hassanzadeh, Pedram (February 2023). "Kolmogorov n–width and Lagrangian physics-informed neural networks: A causality-conforming manifold for convection-dominated PDEs". Computer Methods in Applied Mechanics and Engineering 404: 115810. doi:10.1016/j.cma.2022.115810. 
  28. ↑ Eric Aislan Antonelo; Camponogara, Eduardo; Laio Oriel Seman; Eduardo Rehbein de Souza; Jordanou, Jean P.; Hubner, Jomi F. (2021). "Physics-Informed Neural Nets for Control of Dynamical Systems". arXiv:2104.02556 [cs.LG].
  29. ↑ Wang, Sifan; Teng, Yujun; Perdikaris, Paris (2020-01-13). "Understanding and mitigating gradient pathologies in physics-informed neural networks". arXiv:2001.04536 [cs.LG].

External links

  • PINN – repository to implement physics-informed neural network in Python
  • XPINN – repository to implement extended physics-informed neural network (XPINN) in Python
  • PIPN [2]– repository to implement physics-informed PointNet (PIPN) in Python




Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Physics-informed_neural_networks&oldid=3280962"